Tương tự với số tự nhiên, các phụ huynh và các em thường tự hỏi tập Z là gì, nó có phải là số nguyên không? Bài viết sau sẽ giải đáp các thắc mắc trên một cách chi tiết nhất.
Tập Z là gì?

Tập hợp các số nguyên trong toán học: {0, 1, 2, 3, …} được ký hiệu bằng chữ cái Z.
Z = {0, 1, 2, 3, 4,…}
Số nguyên
Số nguyên là một tập hợp các số bao gồm tất cả các số tự nhiên và 0. Chúng là một phần của số thực không bao gồm phân số, số thập phân hoặc số âm. Người ta coi số đếm cũng là số nguyên.
Số nguyên là gì?
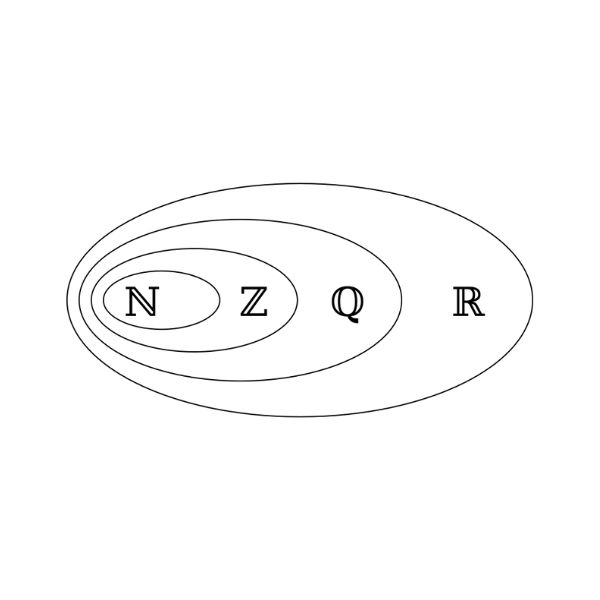
Số tự nhiên đề cập đến một tập hợp các số đếm bắt đầu từ 1 và mặt khác, các số tự nhiên cùng với số không (0) tạo thành một tập hợp, được gọi là số nguyên. Tuy nhiên, số 0 là một danh tính không xác định đại diện cho một tập hợp rỗng hoặc không có kết quả nào cả. Nói cách đơn giản, số nguyên là một tập hợp các số không có phân số, số thập phân hoặc thậm chí là số nguyên âm.
Nó là một tập hợp các số nguyên dương và số không. Hoặc chúng ta có thể nói rằng các số nguyên là tập hợp các số nguyên không âm. Sự khác biệt cơ bản giữa số tự nhiên và số nguyên là sự hiện diện của số 0 trong tập hợp số nguyên.
Định nghĩa
Số nguyên là tập hợp các số tự nhiên cùng với số 0.
Dưới đây là một số kiến thức cơ bản về số nguyên, sẽ giúp bạn hiểu rõ hơn về chúng:
- Mỗi một số tự nhiên là một số nguyên.
- Tất cả các số đếm đều là số nguyên.
- Tất cả các số nguyên dương bao gồm cả số 0 đều là số nguyên.
- Mỗi một số nguyên là một số thực.
- Ký hiệu được sử dụng để đại diện cho các số nguyên là bảng chữ cái ‘Z’ viết hoa, Z = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…
Số nguyên nhỏ nhất
Số nguyên bắt đầu từ 0 (từ định nghĩa của số nguyên). Do đó, 0 được xem như là số nguyên nhỏ nhất. Khái niệm số 0 lần đầu tiên được xác định bởi một nhà thiên văn học và toán học người Hindu Brahmagupta vào năm 628. Nói một cách đơn giản, số 0 là một số nằm giữa số dương và số âm trên một trục số. Mặc dù số 0 không mang giá trị nào, nhưng nó được sử dụng như một trình giữ chỗ. Vì vậy, số 0 không phải là số dương cũng không phải là số âm.
Số nguyên so với số tự nhiên
Từ các định nghĩa trên, chúng ta có thể hiểu rằng mọi số nguyên khác 0 đều là một số tự nhiên. Ngoài ra, mọi số tự nhiên đều là một số nguyên. Vì vậy, tập hợp các số tự nhiên là một phần của tập hợp các số nguyên hoặc tập hợp con các số nguyên.
Điểm khác biệt giữa số nguyên và số tự nhiên
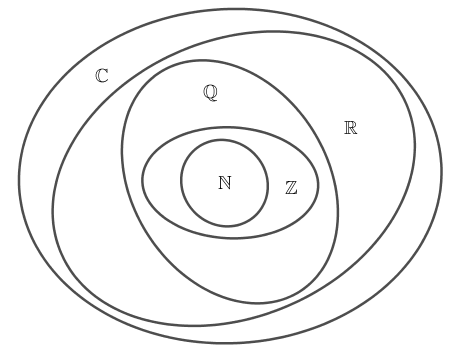
Hãy cùng chúng tôi hiểu sự khác biệt giữa số nguyên và số tự nhiên qua bảng dưới đây:
| Số nguyên | Số tự nhiên |
| Tập hợp các số nguyên là, Z = {0,1,2,3, …}.
|
Tập hợp các số tự nhiên là, N = {1,2,3, …}.
|
| Số nguyên nhỏ nhất bằng 0.
|
Số tự nhiên nhỏ nhất là 1.
|
| Mỗi một số tự nhiên là một số nguyên
|
Mỗi một số nguyên là một số tự nhiên, trừ 0. |
Từ những khác biệt này, chúng ta có thể dễ dàng suy ra rằng mọi số nguyên khác 0 đều là một số tự nhiên. Có thể nói rằng tập hợp các số tự nhiên là một tập hợp con của các số nguyên.
Số nguyên trên trục số
Tập hợp các số tự nhiên và tập hợp các số nguyên có thể được biểu diễn trên trục số như hình dưới đây. Tất cả các số nguyên dương hoặc các số nguyên ở phía bên phải của 0 đại diện cho các số tự nhiên, trong khi tất cả các số nguyên dương cùng với số 0, hoàn toàn đại diện cho các số nguyên. Cả hai bộ số có thể được biểu diễn trên trục số như sau:
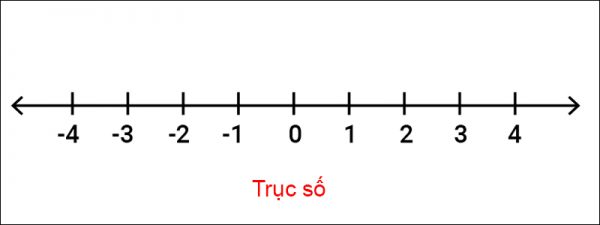
Tính chất của số nguyên
Tính chất tuần hoàn
Tổng và tích của hai số nguyên luôn là một số nguyên.
Ví dụ, 7 + 3 = 10 (số nguyên), 7 × 2 = 14 (số nguyên).
Tính chất kết hợp
Tổng hoặc tích của ba số nguyên bất kỳ vẫn giữ nguyên ngay cả khi nhóm các số bị thay đổi.
Ví dụ, khi cộng các số sau ta được tổng như nhau: 10 + (7 + 12) = (10 + 7) + 12 = (10 + 12) + 7 = 29.
Tương tự, khi nhân các số sau chúng ta nhận được cùng một sản phẩm bất kể các số được nhóm như thế nào: 3 × (2 × 4) = (3 × 2) × 4 = 24.
Tính chất giao hoán
Tổng và tích của hai số nguyên vẫn bằng nhau ngay cả sau khi đổi thứ tự các số. Tính chất này có thể được nói là: sự thay đổi trong thứ tự của phép cộng không làm thay đổi giá trị của tổng.
Gọi ‘a’ và ‘b’ là hai số nguyên. Theo tính chất giao hoán a + b = b + a.
Ví dụ, a = 10 và b = 19 ⇒ 10 + 19 = 29 = 19 + 10.
Tính chất này cũng đúng với phép nhân, nhưng không đúng với phép trừ và phép chia.
Ví dụ: 7 × 9 = 63 và 9 × 7 = 63.
Thức đồng nhất
Khi cộng một số nguyên với 0, giá trị của nó vẫn không thay đổi, tức là nếu x là một số nguyên thì x + 0 = 0 + x = x.
Ví dụ, 3 + 0 = 3 + 0 = 3.
Thức đồng nhất đa nhân
Khi một số nguyên được nhân với 1, giá trị của nó không thay đổi, tức là nếu x là một số nguyên thì x × 1 = x = 1 × x.
Ví dụ. 4 × 1 = 1 × 4 = 4.
Tính chất phân tán
Phép nhân của một số nguyên được phân phối trên tổng hoặc hiệu của các số nguyên. Nó có nghĩa là khi hai số, ví dụ a và b được nhân với cùng một số c và sau đó được thêm vào, thì tổng của a và b có thể được nhân với c để có cùng một đáp số.
Tính chất này có thể được biểu diễn dưới dạng: a × (b + c) = (a × b) + (a × c). Cho a = 10, b = 20 và c = 7 ⇒ 10 × (20 + 7) = 270 và (10 × 20) + (10 × 7) = 200 + 70 = 270.
Tính chất tương tự cũng đúng với phép trừ .
Ví dụ, chúng ta có a × (b – c) = (a × b) – (a × c). Cho a = 10, b = 20 và c = 7 ⇒ 10 × (20-7) = 130 và (10 × 20) – (10 × 7) = 200 – 70 = 130.
Nhân với số 0
Khi một số nguyên được nhân với 0, kết quả luôn là 0, tức là x × 0 = 0 × x = 0. Ví dụ: 4 × 0 = 0.
Chia cho số 0
Phép chia của một số nguyên cho 0 không được xác định, tức là nếu x là số nguyên thì x / 0 không được xác định.
Một số ví dụ có lời giải
Ví dụ 1: 100, 227, 198, 4321 có phải là các số nguyên không?
Lời giải: Có. 100, 227, 198 và 4321 đều là số nguyên.
Ví dụ 2 : Giải 10 × (5 + 10) bằng cách sử dụng thuộc tính phân phối.
Lời giải: Tính chất phân biệt của phép nhân với phép cộng các số nguyên là:
(y + z) × x = (x × y) + (x × z)
6 × (5 + 10) = (6× 5) + (6 × 10)
= 30 + 60
= 90
Do đó, 6 × (5 + 10) = 90
Tuy nhiên, chúng ta có thể đưa ra một số ví dụ về số nguyên bằng cách sử dụng các thuộc tính của số nguyên.
Lưu ý
- 0 là số nguyên nhưng KHÔNG phải là số tự nhiên.
- Số âm, số thập phânvà phân số không phải là số tự nhiên cũng không phải là số nguyên trừ khi chúng có thể được đơn giản hóa dưới dạng số tự nhiên hoặc số nguyên.
- Không có số nguyên ‘lớn nhất’.
- Mọi số nguyên đều có một số trước, ngoại trừ số 0.
- Một số thập phân hoặc một phân số nằm giữa hai số nguyên không phải là một số nguyên.
Mối quan hệ số nguyên và số hữu tỉ
Trong toán học, các số nguyên tạo thành một nhóm nhỏ nhất và vành nhỏ nhất đó sẽ tạo thành các số tự nhiên. Theo lý thuyết đại số thì các số nguyên đó đôi khi được coi là số hữu tỉ để bạn dễ dàng phân biệt được với các số nguyên đại số tổng quát hơn. Trong thực tế, số nguyên (hữu tỉ) là số nguyên đại số và cũng đồng thời là số hữu tỉ. Chúng ta có thể theo dõi tính chất cơ bản của số nguyên theo bảng sau:
| Phép cộng | Phép nhân | |
| Tính đóng | 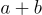 |
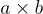 |
| Tính kết hợp | 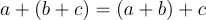 |
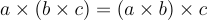 |
| Tính giao hoán | 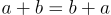 |
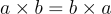 |
| Phần tử đơn vị | 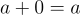 |
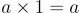 |
| Phần tử nghịch đảo | 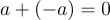 |
Số nguyên duy nhất có phần tử nghịch đảo là -1 và 1 |
| Thuộc tính phân phối | 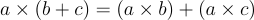 và và 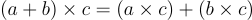 |
|
| Không có ước của số 0 | Nếu 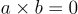 , thì , thì 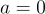 hoặc hoặc 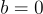 hoặc cả hai. hoặc cả hai. |
|
Thuộc tính về lý thuyết thứ tự
Tập hợp Z là một tập hợp số không có bất kì giới hạn trên hay dưới. Ví dụ về thứ tự của tập hợp Z được hiểu như sau:  .
.
Một số nguyên dương khi nó lớn hơn 0 và nguyên âm khi nó nhỏ hơn 0.
Số 0 là số trung gian và nó không âm cũng không dương.
Từ thứ tự của các số nguyên ta có tính chất sau:
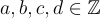 thì chúng ta có hai tính chất:
thì chúng ta có hai tính chất:
- Nếu
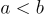 và
và 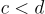 thì
thì 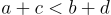
- Nếu
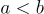 và
và 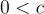 thì
thì 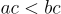
Do các tính chất đó, người ta kết luận rằng Z cùng với thứ tự trên là một vành có thứ tự.
Câu hỏi ôn tập lại lý thuyết
Câu 1: Lấy VD thực tế trong đó có số nguyên âm, giải thích ý nghĩa của số nguyên âm đó.
Câu 2: Tập hợp Z các số nguyên bao gồm những số nào?
Câu 3: Cho biết trên trục số hai số đối nhau có đặc điểm gì?
Câu 4: Nói tập hợp Z bao gồm hai bộ phận là số tự nhiên và số nguyên âm đúng không?
Câu 5: Nhắc lại cách so sánh hai số nguyên a và b trên trục số?
Bài tập về tập hợp số nguyên
Để kết thúc lại chuyên đề này, chúng ta cùng tìm hiểu một số
Bài 1: Cho tập hợp 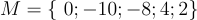
Đề bài
a/ Viết tập hợp N gồm các phần tử là số đối của các phần tử thuộc tập M.
b/ Viết tập hợp P gồm các phần tử của M và N
Đáp án
a) 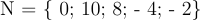
b) 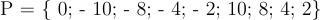
Bài 2: Trong các câu sau câu nào đúng? Câu nào sai?
Đề bài
a/ Mọi số tự nhiên đều là số nguyên.
b/ Mọi số nguyên đều là số tự nhiên.
c/ Có những số nguyên đồng thời là số tự nhiên.
d/ Có những số nguyên không là số tự nhiên.
e/ Số đối của 0 là 0, số đối của a là (–a).
g/ Khi biểu diễn các số (-5) và (-3) trên trục số thì điểm (-3) ở bên trái điểm (-5).
h/ Có những số không là số tự nhiên cũng không là số nguyên.
Đáp án
ĐS: Các câu sai: b/ g/
Bài 3: Trong các câu sau câu nào đúng? Câu nào sai?
Đề bài
a/ Bất kỳ số nguyên dương nào xũng lớn hơn số nguyên ân.
b/ Bất kỳ số tự nhiên nào cũng lớn hơn số nguyên âm.
c/ Bất kỳ số nguyên dương nào cũng lớn hơn số tự nhiên.
d/ Bất kỳ số tự nhiên nào cũng lớn hơn số nguyên dương.
e/ Bất kỳ số nguyên âm nào cũng nhỏ hơn 0.
Đáp án
ĐS: Các câu sai: d/
Bài 4: Sắp xếp số nguyên
Đề bài
a/ Sắp xếp các số nguyên sau theo thứ tự tăng dần: 2, 0, -1, -5, -17, 8
b/ Sắp xếp các số nguyên sau theo thứ tự giảm dần: -103, -2004, 15, 9, -5, 2004
Đáp án
a/ -17. -5, -1, 0, 2, 8
b/ 2004, 15, 9, -5, -103, -2004
Bài 5: Trong các cách viết sau, cách viết nào đúng?
Đề bài
a/ -3 < 0
b/ 5 > -5
c/ -12 > -11
d/ |9| = 9
e/ |-2004| < 2004
f/ |-16| < |-15|
Đáp số
Các câu sai: c/ e/ f/
Bài 6: Tìm x
Đề bài
a/ |x – 5| = 3
b/ |1 – x| = 7
c/ |2x + 5| = 1
Hướng dẫn
a/ |x – 5| = 3 nên x – 5 = ± 3
- x – 5 = 3 ➡ x = 8
- x – 5 = -3 ➡ x = 2
b/ |1 – x| = 7 nên 1 – x = ± 7
- 1 – x = 7 ➡ x = -6
- 1 – x = -7 ➡ x = 8
c/ x = -2, x = 3
Bài 7: So sánh các số sau
Đề bài
a) So sánh 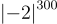 và
và 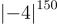
b) So sánh 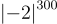 và
và 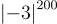
Đáp án
a)
Ta có 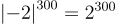
Ta có 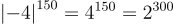
Do đó 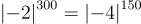
b)
Ta có 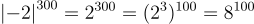
Ta có 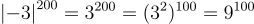
Vì 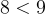 nên
nên 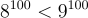
Do đó 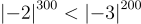
Tóm lại, chúng ta có thể nói rằng tập Z là một tập hợp của số nguyên, là một phần quan trọng của hệ thống số bao gồm tất cả các số nguyên dương từ 0 đến vô cùng.
Qua bài viết trên chúng ta đã tìm hiểu tập Z là gì, các khái niệm, tính chất cũng như những điểm khác biệt so với số tự nhiên. Chúc các bạn nhận được điểm cao trong bài thi!