Tập hợp có mặt ở khắp mọi nơi trong toán học hiện đại. Quả thực, những lý thuyết về tập hợp đã là phương pháp tiêu chuẩn để cung cấp những kiến thức chặt chẽ cho hầu đa tất cả các phân nhánh của toán học tính từ nửa đầu thế kỷ 20 cho tới nay.
Tập hợp, biểu đồ ven có lẽ là những khái niệm khá quen thuộc mà chúng ta đã học ngay từ bài đầu tiên làm quen với các tập hợp số tự nhiên, số nguyên, số hữu tỉ số vô tỉ, số thực, trong chương trình toán của THCS.
Bài viết sau giới thiệu đến các bạn tập hợp là gì? Ngoài ra sẽ có những thông tin về các phép toán tập hợp và những dạng bài thường gặp.
Khái niệm
Trong toán học, Tập hợp có thể được hiểu là một sự tụ tập của một số vô hạn hay hữu hạn những đối tượng nào đó. Những đối tượng này được gọi là phần tử của tập hợp.
Các phần tử để tạo nên một tập hợp có thể là bất kỳ những loại đối tượng nào: số, các điểm trong không gian, ký hiệu, hay đường thẳng, những hình dạng hình học khác, các biến hoặc thậm chí có thể là những tập hợp khác.
Một tập hợp này có thể được coi là phần tử của một tập hợp khác. Tập hợp trong đó mỗi phần tử của nó là một tập nhỏ hơn hợp lại còn được gọi là họ tập hợp.
Một tập hợp có thể có nhiều phần tử hoặc thậm chí không có phần tử nào.
Ví dụ:
- “Tập hợp các số tự nhiên chia hết cho 4 và nhỏ hơn 30” : Tập hợp các số tự nhiên thỏa mãn các tính chất: vừa chia hết cho 4 và nhỏ hơn 30.
- Tập hợp những cuốn sách học tiếng anh lớp 7 được mua nhiều nhất
- Tập hợp học sinh trường THPT ABC
- Tập hợp các số từ 1 đến 100
Ký Hiệu Và Biểu Diễn
Các mục dưới đây sẽ nói rõ hơn về cách biểu diễn tập hợp và các ký hiệu thường sử dụng trong tập hợp toán học.
Ký Hiệu
Tập hợp được kí hiệu bằng chữ cái in hoa. Ghi các phần tử trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu , hay ;
Phần tử a thuộc tập hợp A: a ∈ A.
Phần tử a không thuộc tập hợp A: a∉ A
Biểu diễn
Mỗi tập hợp bao gồm hai phần, thứ nhất là tên, thứ hai là danh sách các phần tử của tập hợp. Tên tập hợp được dùng để phân biệt với các tập khác, phải là duy nhất và tên không được trùng với tập hợp khác.
Ví dụ: Hãy biểu diễn tập hợp các số tự nhiên bé hơn 5.
Gọi B là tập hợp các số tự nhiên bé hơn 5, lúc này ta biểu diễn như sau:
A = {0;1;2;3;4}
Ví dụ 2: Tập hợp các chữ cái in hoa A, B, C, D, E, F.
Gọi k là tập hợp các chữ cái A,B,C,D, E, F. Lúc này ta biểu diễn như sau:
N = {A,B,C,D, E, F}
Lưu ý:
- Có thể liệt kê tùy ý thứ tự các phần tử
- Mỗi phần tử chỉ được liệt kê duy nhất 1 lần
- Thường sử dụng chữ cái in hoa để biểu diễn tên tập hợp
Cách cho một tập hợp
Một tập hợp được xác định bằng cách chỉ ra những tính chất đặc trưng cho các phần tử của nó. Do vậy chúng ta có thể xác định một tập hợp bằng 2 cách như sau:
Liệt kê lần lượt các phần tử : C = {phần tử}
Chỉ ra tính chất đặc trưng của các phần tử đó (Chỉ rõ tính chất đặc trưng của các phần tử sẽ giúp thâu tóm ngắn gọn những tập hợp dài.)
Một tập hợp mà không có phân tử nào được gọi là tập hợp rỗng, kí hiệu là Ø.
Mỗi tập hợp đều là tập hợp con của chính nó, ta có quy ước: tập hợp rỗng là tập hợp con của tất cả mọi tập hợp.
Biểu diễn tập hợp cơ bản
Theo cách cơ bản, chúng ta sẽ liệt kê lần lượt các phần tử có trong tập hợp.
Ví dụ như sau:
Biểu diễn tập hợp A, A gồm các số từ 0 đến 4. Tập hợp A biểu diễn như sau:
A = {0; 1; 2; 3}
Biểu diễn tập hợp nâng cao
Tùy vào từng dạng bài toán mà chúng ta sẽ có những cách biểu diễn cơ bản hoặc nâng cao.
Ví dụ như sau:
N là tập hợp những [số tự nhiên] (tức là các số từ 0 trở về sau).
Biểu diễn tập hợp A , A bao gồm các số từ 0 đến 4. Lúc này chúng ta sẽ biểu diễn như sau:
A = {x∈ N | x < 5}, với N là tập hợp các số tự nhiên.
=> Tập hợp A bao gồm các số x thuộc tập hợp các số tự nhiên N, trong đó điều kiện là x phải bé hơn 5.
Tóm lại để viết biểu diễn tập hợp thì ta có hai cách thông dụng như sau:
Cách cơ bản: Liệt kê lần lượt ra tất các phần tử
Cách nâng cao: Dựa vào những tính chất đặc trưng của tập hợp mà sẽ biểu diễn nâng cao
Biểu diễn tập hợp bằng hình
Biểu diễn tập hợp bằng hình là cách biểu diễn thường gặp trong các bài tập toán. Để có thể biểu diễn bằng hình, chúng ta dùng một hình tròn chứa tất cả các phần tử của 1 tập hợp, sau đó dùng một mũi tên trỏ chỉ đến tên của tập hợp.
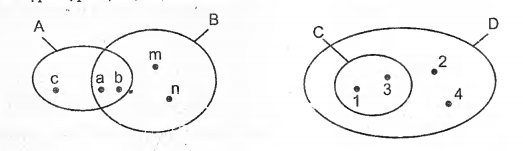
A gồm các phần tử: a, b, c: A = {a, b, c}
B gồm các phần tử a, b, m, n: B = {a, b, m, n}
Một Số Tập Hợp Cơ Bản
Tập hợp của các số tự nhiên có ký hiệu quy ước là N
N={0, 1, 2, 3, 4, 5, 6, 7, 8 ..}
Tập hợp của các số nguyên có ký hiệu quy ước là Z
Z={…-4, -3, -2, -1, 0, 1, 2, 3, …}
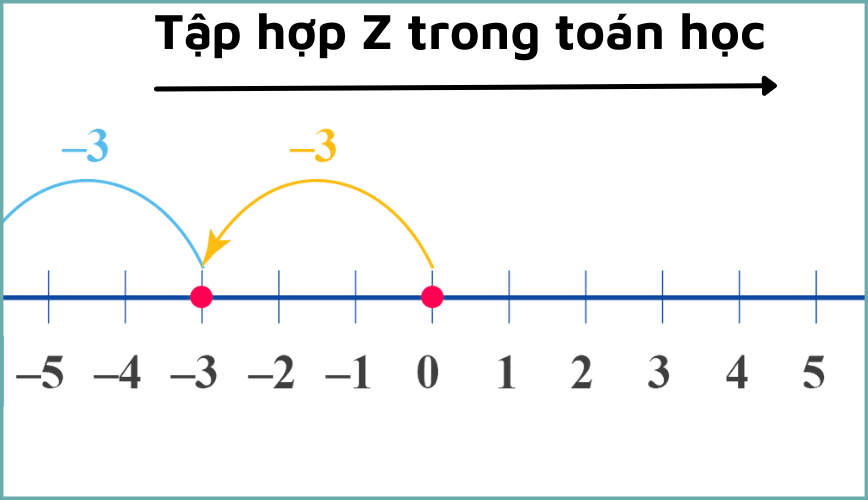
Tập hợp số nguyên bao gồm các phân tử là các số tự nhiên và các phần tử là số đối của các số tự nhiên đó.
Tập hợp của các số nguyên dương có ký hiệu quy ước là là N*
Tập hợp của các số hữu tỉ,có ký hiệu quy ước là Q
Q={ a/b; a, b∈Z, b≠0}
Số hữu tỉ có thể được biểu diễn bằng một số thập phân hữu hạn hoặc một số thập phân vô hạn tuần hoàn.
Tập hợp của các số thực có ký hiệu quy ước là R
Mỗi số sẽ được biểu diễn bằng một số vô tỉ, là số thập phân vô hạn không tuần hoàn. Tập hợp các số vô tỉ có kí hiệu là I. Số thực sẽ bao gồm tập hợp các số hữu tỉ và các số vô tỉ.
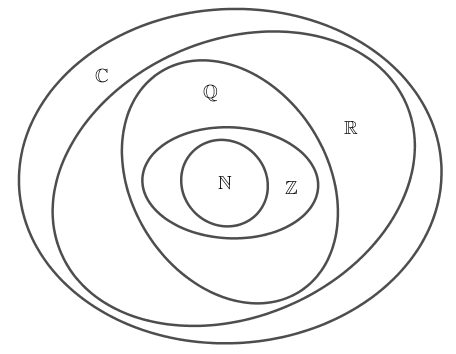
Mối Quan Hệ Giữa Các Tập Hợp Số
Tập hợp con
Chúng ta gọi A là tập hợp con của B nếu mọi phần tử của A đều thuộc B, được kí hiệu như sau:
A ⊂ B ⇔ x ∈ A => x ∈ B
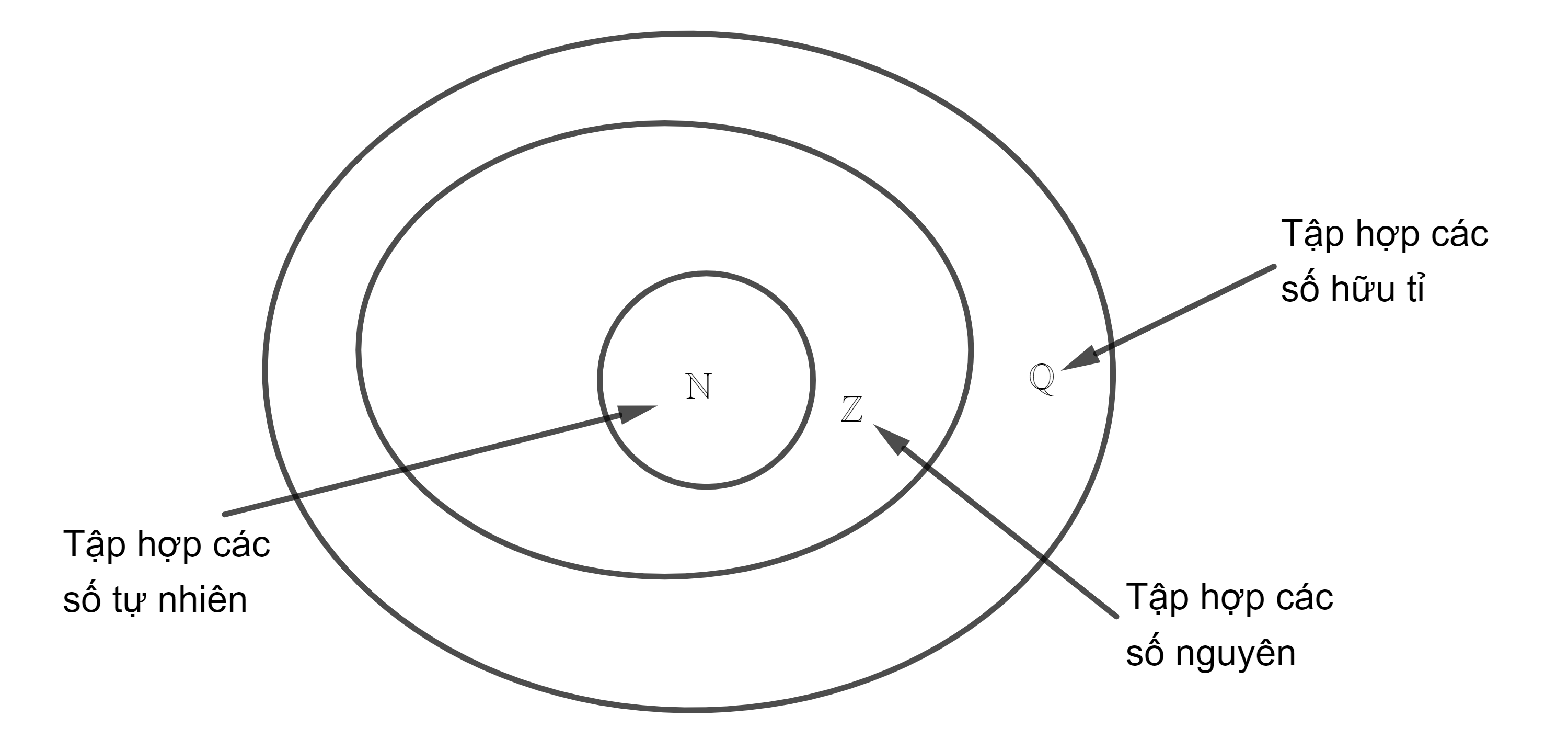
Quan hệ bao hàm giữa các tập hợp số với nhau là : N ⊂ Z ⊂ Q ⊂ R
Hai tập hợp bằng nhau
Nếu tất cả các phần tử của tập hợp A và tập hợp B đều như nhau, hai tập hợp này được gọi là bằng nhau và kí hiệu là A = B. Biểu thị như sau:
A = B ⇔ A ⊂ B và B ⊂ A.
Biểu đồ Ven
Người ta thường dùng một đường cong khép kín được giới hạn trên một phần của mặt phẳng để minh họa một tập hợp. Các điểm nằm trên phần mặt phẳng này được dùng để biểu thị các phần tử của tập hợp ấy.
Mối quan hệ giữa các tập hợp số được thể hiện một cách trực quan qua biểu đồ Ven.

Các Phép Toán Với Tập Hợp
Phép giao
Giao của hai tập hợp A và B, kí hiệu A ∩ B, đây là tập hợp gồm các phần tử thuộc tập hợp B. Biểu diễn như sau:
A ∩ B = {x/ x ∈ A và x ∈ B}.
Phép hợp
Phép hợp của hai tập hợp A, tập hợp B, kí hiệu là A ∪ B. Đây là tập hợp gồm các phần tử hoặc thuộc A, hoặc thuộc B. Biểu diễn như sau:
A ∪ B = {x/ x ∈ A hoặc x ∈ B}.
Phép hiệu
Hiệu của tập A với tập B, kí hiệu A\B, Đây là tập hợp gồm các phần tử thuộc tập A và không thuộc tập B. Biểu diễn như sau:
A\B= {x/ x ∈ A và x ∉ B}.
Phần bù
Nếu B ⊂ A thì AB gọi là phần bù của B trong A. Kí hiệu là CAB
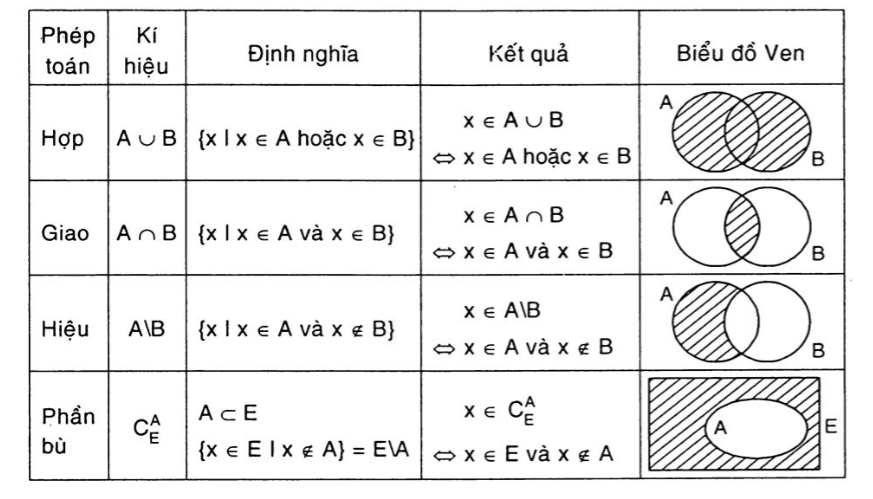
Ví dụ minh họa các phép toán:
Với A là tập hợp các chữ cái trong câu tục ngữ “CÓ CHÍ THÌ NÊN”, còn B là tập hợp các chữ cái của câu tục ngữ “CÓ CÔNG MÀI SẮT CÓ NGÀY NÊN KIM’.
Xác định các phần tử của: A ∩ B, A ∪ B, A\B, B\A
Lời giải của ví dụ này như sau:
A= { I, N, O, T, C, Ê, H}
B = { K, I, G, O, Ô, A, Ă, C, Ê, M, N, S, T, Y}
A ∩ B = { N, O, T, C, Ê, I}
A ∪ B = { G, H, I, K, M, A, Ă, C, E, Ê, N, O, Ô, S, T, Y}.
A\B = {H}.
B\A = (M,S,Y,K, A,Ă,G,Ô)
Ví Dụ 2:
Cho tập hợp A, hãy xác định
A ∩ A, A ∪ A, A ∩ Ø, A ∪ Ø
Lời giải của ví dụ này như sau:
A ∩ A = A;
A ∪ A = A;
A ∩ Ø = Ø;
A ∪ Ø = A;
Một số dạng toán ứng dụng phép toán tập hợp
Dạng 1: Xác định tập hợp và những phép toán trên tập hợp
Ví dụ:
Cho A là tập hợp các học sinh khối 11 đang học ở trường và B là tập hợp các học sinh đang học môn Văn ở trường. Diễn đạt bằng lời cho các tập hợp sau: A∪B;A∩B;A∖B;B∖A.
- A∪B: tập hợp các học sinh hoặc đang học lớp 11, hoặc đang học môn Văn ở trường.
- A∩B: tập hợp các học sinh lớp 11 học môn Văn ở trường.
- A∖B: tập hợp các học sinh đang học lớp 11 nhưng không học môn Văn ở trường.
- B∖A: tập hợp các học sinh học môn Văn ở trường nhưng không học lớp 11.
Dạng 2: Vận dụng biểu đồ Ven để giải toán tập hợp
Để sử dụng biểu đồ ven để giải toán tập hợp, chúng ta làm theo 3 bước như sau:
- Chuyển bài toán dưới dạng ngôn ngữ tập hợp.
- Vận dụng sơ đồ Ven minh họa các tập hợp trên.
- Dựa vào sơ đồ Ven chúng ta thiết lập được đẳng thức, phương trình hoặc hệ phương trình, và từ đó tìm ra kết quả bài toán.
Dạng 3: Các phép toán trên tập hợp con của các tập số thực
- Phép A∩B, ta làm như sau
– Sắp xếp lên trục số theo thứ tự tăng dần các điểm đầu mút các tập hợp A, B
– Biểu diễn các tập A, tập B trên trục số (phần nào không thuộc các tập hợp do thì gạch bỏ)
– Phần không bỏ chính là giao của hai tập hợp A, B
- Phép A U B, ta làm như sau
– Sắp xếp lên trục số theo thứ tự tăng dần các điểm đầu mút của các tập hợp A, B
– Tô đậm các tập hợp A, tập B trên trục số
– Phần tô đậm là hợp của hai tập hợp A, B
- Phép A∖B,ta ta làm như sau
– Sắp xếp lên trục số theo thứ tự tăng dần các điểm đầu mút của các tập hợp A, B
Biểu diễn các tập A trên trục số (gạch phần không thuộc A ). gạch phần thuộc B
– Phần không bị gạch là A \ B
Bài viết trên đây đã chia sẻ đến bạn đọc về Tập hợp là gì? Ngoài ra còn cung cấp thêm thông tin về những phép toán và những dạng bài thông dụng về tập hợp. Hy vọng đó là những thông tin hữu ích cho việc học toán của bạn.