Chắc hẳn những phụ huynh nuôi dạy con tại nhà sẽ gặp khó khăn khi tìm hiểu số tự nhiên. Trong bài viết sau, chúng ta sẽ đi sâu vào tìm hiểu khái niệm số tự nhiên là gì và các định nghĩa, tính chất của nó ?
Giới thiệu về Số tự nhiên

Những con số luôn ở khắp mọi nơi xung quanh chúng ta, để đếm đồ vật, đại diện hoặc đổi tiền, để đo nhiệt độ, cho biết thời gian, v.v. Những con số được sử dụng để đếm được gọi là “số tự nhiên”. Ví dụ, trong khi đếm đồ vật, chúng ta nói 5 cái cốc, 6 cuốn sách, 1 cái chai, v.v.
Số tự nhiên
Số tự nhiên bao gồm tất cả các số nguyên dương từ 1 đến vô cùng, là một phần trong hệ thống số.
Số tự nhiên còn có cách gọi khác là số đếm vì chúng không chứa số 0 hoặc số âm. Chúng là một phần của số thực chỉ bao gồm các số nguyên dương, nhưng không chứa số 0, phân số, số thập phân và số âm.
Số tự nhiên là gì?
Số tự nhiên đề cập đến một tập hợp tất cả các số nguyên không bao gồm 0. Những con số này được ứng dụng thường xuyên trong các hoạt động hàng ngày của chúng ta.
Định nghĩa số tự nhiên
Số tự nhiên là là một phần của số thực và được dùng để đếm. Tập hợp các số tự nhiên chỉ có duy nhất các số nguyên dương, tức là 1, 2, 3, 4, 5, 6, ……… .∞.
Ví dụ về số tự nhiên
Số tự nhiên còn có tên gọi khác là số nguyên không âm (vì nó chứa tất cả các số nguyên dương). Một số ví dụ bao gồm 23, 56, 78, 999, 100202, v.v.
Tập hợp các số tự nhiên

Tập hợp là một tập hợp các phần tử (các số trong ngữ cảnh này). Tập hợp các số tự nhiên trong Toán học được viết là {1,2,3, …}. Ký hiệu của tập hợp các số tự nhiên là chữ cái N.
N = {1,2,3,4,5, … ∞}
Dạng phát biểu N = Tập hợp tất cả các số bắt đầu từ 1.
Dạng viết: N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………}
Đặt biểu mẫu trình tạo N = {x: x là một số nguyên bắt đầu từ 1}
Số tự nhiên nhỏ nhất
Số tự nhiên nhỏ nhất là 1. 1 là phần tử nhỏ nhất trong N và cùng với mọi phần tử trong N, ta phát biểu với phần tử tiếp theo là là 1 và N (nhiều hơn phần tử đó 1 phần tử).
Ví dụ: hai là một hơn một, ba là một hơn hai, v.v.
Số tự nhiên từ 1 đến 100

Các số tự nhiên từ 1 đến 100 là 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 và 100.
Số 0 không phải là số tự nhiên
Không, vì số tự nhiên là số đếm nên 0 KHÔNG phải là số tự nhiên. Để bắt đầu đếm số lượng bất kỳ đối tượng nào, chúng ta đếm từ 1 chứ không phải từ 0.
Số tự nhiên lẻ
Các số tự nhiên lẻ là các số thuộc tập N và là các số lẻ. Vậy tập các số tự nhiên lẻ là {1,3,5,7, …}.
Số tự nhiên chẵn
Các số tự nhiên chẵn là các số thuộc tập N và là số chẵn chia hết cho 2. Vậy tập hợp các số tự nhiên chẵn là {2,4,6,8, …}.
Số tự nhiên và Số nguyên
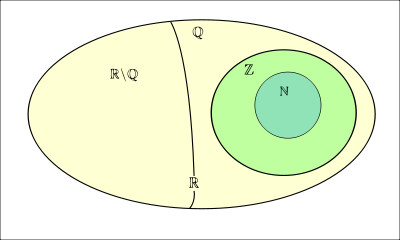
Tập hợp các số nguyên giống như tập hợp các số tự nhiên, chỉ khác là nó có thêm một số là 0. Tập hợp các số nguyên trong Toán học được viết là {0,1,2,3, …}. Ký hiệu của tập hợp số nguyên là chữ cái Z.
Z = {0,1,2,3,4…}
Từ các định nghĩa trên, chúng ta có thể hiểu rằng mọi số tự nhiên đều là một số nguyên. Ngoài ra, mọi số nguyên khác 0 đều là số tự nhiên. Có thể nói rằng tập hợp các số tự nhiên là một tập hợp con của tập hợp các số nguyên.
Điểm khác biệt giữa số tự nhiên và số nguyên
Số tự nhiên là tất cả các số dương như 1, 2, 3, 4, v.v. Chúng là những con số tiếp tục cho đến vô tận mà bạn thường đếm. Trong khi, các số nguyên là tất cả các số tự nhiên bao gồm 0, chẳng hạn như 0, 1, 2, 3, 4, v.v. Số nguyên bao gồm tất cả các số nguyên và phần đối âm của chúng. ví dụ: -4, -3, -2, -1, 0,1, 2, 3, 4, v.v. Bảng sau đây cho thấy sự khác biệt giữa một số tự nhiên và một số nguyên.
|
Số tự nhiên |
Số nguyên
|
|
Tập hợp các số tự nhiên là N = {1,2,3, … ∞}
|
Tập hợp các số nguyên là W = {0,1,2,3, …} |
|
Số tự nhiên nhỏ nhất là 1.
|
Số nguyên bé nhất bằng 0.
|
| Tất cả các số tự nhiên đều là số nguyên, nhưng tất cả các số nguyên không phải là số tự nhiên.
|
Mỗi số nguyên là một số tự nhiên, trừ số 0. |
Số tự nhiên trên trục số
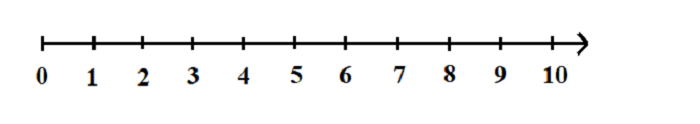
Tập hợp các số tự nhiên và các số nguyên có thể được biểu diễn trên trục số như hình dưới đây. Các số ở phía bên phải của 0, toàn bộ các số nguyên dương hoặc các số nguyên đại diện cho các số tự nhiên. Trong khi tất cả các số nguyên dương cùng với số 0 đại diện cho các số nguyên.
Tính chất của số tự nhiên
Tính chất tuần hoàn
Tích và tổng của hai số tự nhiên luôn là một số tự nhiên.
Tính chất tuần hoàn của phép cộng: a + b = c ⇒ 1 + 2 = 3, 7 + 8 = 15. Điều này cho thấy tổng của các số tự nhiên luôn là một số tự nhiên.
Tính chất tuần hoàn của phép nhân: a × b = c ⇒ 2 × 3 = 6, 7 × 8 = 56, v.v. Điều này cho thấy tích của các số tự nhiên luôn là một số tự nhiên.
Vì vậy, tập hợp các số tự nhiên, N tuần hoàn dưới phép cộng và phép nhân nhưng điều này không đúng trong phép trừ và phép chia.
Tính chất kết hợp
Tổng hoặc tích của ba số tự nhiên ngẫu nhiên vẫn giữ nguyên ngay cả khi nhóm các số bị thay đổi.
Tính chất kết hợp của phép cộng: a + (b + c) = (a + b) + c ⇒ 2+ (3 + 1) = 2 + 4 = 6 và kết quả tương tự thu được trong (2 + 3) + 1 = 5 + 1 = 6.
Tính chất kết hợp của phép nhân: a × (b × c) = (a × b) × c ⇒ 2 × (3 × 1) = 2 × 3 = 6 = và kết quả tương tự thu được trong (a × b) × c = (2 × 3) × 1 = 6 × 1 = 6.
Vì vậy, tập hợp các số tự nhiên, N có thể kết hợp trong phép cộng và phép nhân nhưng điều này không xảy ra trong trường hợp trừ và chia.
Tính chất giao hoán
Kể cả sau khi đổi thứ tự các số, tổng hoặc tích của hai số tự nhiên đều không đổi.
Tính chất giao hoán của N là: Với mọi a, b∈N: a + b = b + a và a × b = b × a.
Tính chất giao hoán của phép cộng: a + b = b + a ⇒ 8 + 9 = 17 và b + a = 9 + 8 = 17.
Tính chất giao hoán của phép nhân: a × b = b × a ⇒ 8 × 9 = 72 và 9 × 8 = 72.
Vì vậy, tập hợp các số tự nhiên, N giao hoán trong phép cộng và phép nhân nhưng không giao hoán trong phép trừ và phép chia.
Chúng ta hãy tóm tắt ba tính chất này của số tự nhiên trong một bảng. Vì vậy, tập hợp các số tự nhiên, N là giao hoán trong phép cộng và phép nhân.
| Tính chất tuần hoàn | Tính chất kết hợp | Tính chất giao hoán | |
| Phép cộng | có | có | có |
| Phép trừ
|
không | không | không |
| Phép nhân | có | có | có |
| Phép chia | không | không | không |
Tính chất phân phối
Tính chất phân phối của phép nhân với phép cộng là a × (b + c) = a × b + a × c
Tính chất phân phối của phép nhân với phép trừ là a × (b − c) = a × b − a × c
Ví dụ minh họa và lời giải
Câu 1: Tính chất giao hoán và tính chất kết hợp là các tính chất của cả số tự nhiên và số nguyên. Đúng hay sai? Tại sao?
Lời giải: Số tự nhiên và số nguyên đều tuân theo tính chất giao hoán và tính chất kết hợp.
- Tính chất giao hoán:
Phép cộng: a + b = b + a
Phép nhân: a × b = b × a
- Tính chất kết hợp:
Phép cộng: (a + b) + c = a + (b + c)
Phép nhân: b × (a × c) = (a × b) × c
Câu 2: Từ các chữ số 0, 1, 2, 3 có thể lập được bao nhiêu số tự nhiên có hai chữ số nếu không lặp lại các chữ số trong các số này?
Lời giải: Số tự nhiên có 2 chữ số mà không lặp lại các chữ số trên là: 10,12,13,20,21,23,30,31,32.
Lưu ý
- 0 không phải là số tự nhiên, nó là số nguyên.
- Số âm, số thập phân và phân số không là số tự nhiên cũng không là số nguyên.
- N tuần hoàn, kết hợp và giao hoán trong cả phép cộng và phép nhân (nhưng không dưới phép trừ và phép chia).
Bài viết trên đã tổng hợp tất cả các kiến thức cơ bản về khái niệm số tự nhiên là gì, các định nghĩa và tính chất cũng như những lưu ý cần biết. Chúc các bạn học tốt!